Simpson rule - Numerical Analysis

#%config InlineBackend.figure_format = 'svg'
from pylab import *
from scipy.interpolate import barycentric_interpolate

9.4.1Single interval¶

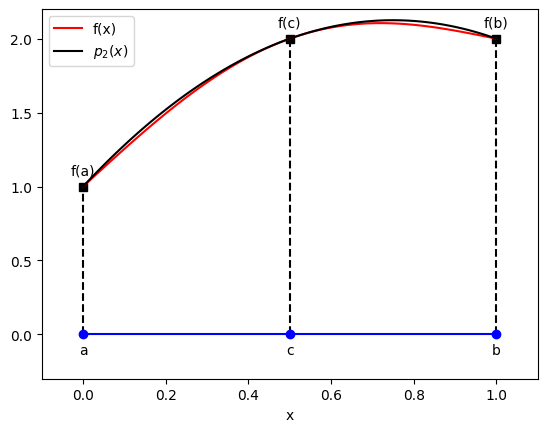
Trapezoidal method used a linear approximation to estimate the integral. To improve the accuracy, let us use a quadratic approximation. For the function $f : [a,b] \to \re$ , we first construct a quadratic polynomial $p_2(x)$ that interpolates at $a, b, c = \half(a+b)$

p_2(a) = f(a), \qquad p_2(b) = f(b), \qquad p_2(c) = f(c)

(1)

and the approximation to the integral is

I_2(f) = \int_a^b p_2(x) \ud x = \frac{h}{3}[f(a) + 4 f(c) + f(b)], \qquad h = \half(b-a)

(2)

This is called Simpson rule.

a, b = 0.0, 1.0
c    = 0.5*(a + b)
f = lambda x: 1.0 + x + 0.5 * sin(pi*x)
x = linspace(a,b,100)
plot([a,a],[0,f(a)],'k--')
plot([b,b],[0,f(b)],'k--')
plot([c,c],[0,f(c)],'k--')
plot([a,c,b],[0,0,0],'bo-')
plot([a,c,b],[f(a),f(c),f(b)],'sk')
plot(x, f(x), 'r-', label='f(x)')
plot(x,barycentric_interpolate([a,c,b],[f(a),f(c),f(b)],x),'k-',
     label='$p_2(x)$')
d = 0.06
text(a,-d,"a",ha='center',va='top')
text(b,-d,"b",ha='center',va='top')
text(c,-d,"c",ha='center',va='top')
text(a,f(a)+d,"f(a)",ha='center',va='bottom')
text(b,f(b)+d,"f(b)",ha='center',va='bottom')
text(c,f(c)+d,"f(c)",ha='center',va='bottom')
axis([-0.1, 1.1, -0.3, 2.2])
legend(), xlabel('x');

The error in the integral follows from polynomial interpolation error (30)

\begin{align} E_2(f) &= I(f) - I_2(f) \\ &= \int_a^b [f(x) - p_2(x)] \ud x \\ &= \int_a^b \underbrace{(x-a)(x-c)(x-b)}_{\textrm{changes sign at $x=c$}} f[a,b,c,x] \ud x \end{align}

(3)

We cannot apply the integral mean value theorem like we did for trapezoid rule. Define

w(x) = \int_a^x (t-a)(t-c)(t-b)\ud t

(4)

Then

w(a) = w(b) = 0, \qquad w(x) > 0, \quad \forall x \in (a,b)

(5)

and

w'(x) = (x-a)(x-c)(x-b)

(6)

Hence the error can be written as

\begin{aligned} E_2(f) &= \int_a^b w'(x) f[a,b,c,x] \ud x \\ &= \left[ w(x) f[a,b,c,x] \right]_a^b - \int_a^b w(x) \dd{}{x} f[a,b,c,x] \ud x \\ &= - \int_a^b w(x) f[a,b,c,x,x] \ud x \end{aligned}

(7)

where we used result from Section 7.7.10 on derivative of divided differences. Now we can apply the integral mean value theorem

\begin{aligned} E_2(f) &= -f[a,b,c,\xi,\xi] \int_a^b w(x) \ud x, \quad \textrm{for some $\xi \in [a,b]$} \\ &= -\frac{1}{24} f^{(4)}(\eta) \left[ \frac{4}{15} h^5 \right], \quad \textrm{for some $\eta \in [a,b]$} \end{aligned}

(8)

The error in Simpson rule is given by

E_3(f) = -\frac{1}{90} h^5 f^{(4)}(\eta), \quad \textrm{for some $\eta \in [a,b]$}

(9)

and

I(f) = I_n(f) -\frac{1}{90} h^5 f^{(4)}(\eta), \quad \textrm{for some $\eta \in [a,b]$}

(10)

9.4.2Composite Simpson rule¶

Let $n \ge 2$ be even, the spacing between points $h = (b-a)/n$ and the $n+1$ points

x_j = a + j h, \quad j=0,1,2,\ldots,n

(11)

In the interval $[x_{2j-2}, x_{2j}]$ , we have the three points $\{ x_{2j-2}, x_{2j-1}, x_{2j} \}$ using which we can apply Simpson rule. Then

\begin{aligned} I(f) &= \int_a^b f(x) \ud x \\ &= \sum_{j=1}^{n/2} \int_{x_{2j-2}}^{x_{2j}} f(x) \ud x \\ &= \sum_{j=1}^{n/2}\left\{ \frac{h}{3}[f_{2j-2} + 4 f_{2j-1} + f_{2j}] - \frac{h^5}{90} f^{(4)}(\eta_j) \right\}, \quad \eta_j \in [x_{2j-2},x_{2j}] \end{aligned}

(12)

The composite Simpson rule is

I_n(f) = \frac{h}{3}[ f_0 + 4 f_1 + 2 f_2 + \ldots + 2 f_{n-2} + 4 f_{n-1} + f_n]

(13)

The error in this approximation is

E_n(f) = I(f) - I_n(f) = -\frac{h^5}{90} \left(\frac{n}{2}\right) \clr{red}{ \left[ \frac{2}{n} \sum_{j=1}^{n/2} f^{(4)}(\eta_j) \right] }

(14)

If the fourth derivative is continuous and since $n h = b-a$ , we get

E_n(f) = -\frac{1}{180} (b-a)h^4 \clr{red}{f^{(4)}(\eta)}, \quad \textrm{for some $\eta \in [a,b]$}

(15)

We can also derive the asymptotic error formula

E_n(f) \approx \tilde E_n(f) = -\frac{h^4}{180}[ f^{(3)}(b) - f^{(3)}(a)]

(16)

The following function implements composite Simpson rule.

def simpson(a,b,n,f,df3):
    h = (b-a)/n
    x = linspace(a,b,n+1)
    y = f(x)
    res = 4.0*sum(y[1:n:2]) + 2.0*sum(y[2:n-1:2]) + y[0] + y[n]
    est = -(h**4/180.0)*(df3(b) - df3(a))
    return (h/3.0)*res, est

Example 1

I = \int_0^\pi \ee^x \cos x \ud x = -\half[1 + \exp(\pi)]

(17)

# Function f
f = lambda x: exp(x)*cos(x)
# Third derivative of f
df3 = lambda x: -2.0*exp(x)*(cos(x) + sin(x))

qe = -0.5*(1.0 + exp(pi)) # Exact integral

n,N = 2,10
e = zeros(N)
for i in range(N):
    integral,est = simpson(0.0,pi,n,f,df3)
    e[i] = qe - integral
    if i > 0:
        print('%6d %18.8e %14.5f %18.8e %12.4f' % 
              (n,e[i],e[i-1]/e[i],est,est/e[i]))
    else:
        print('%6d %18.8e %14.5f %18.8e %12.4f' % (n,e[i],0,est,est/e[i]))
    n = 2*n

     2    -4.77506763e-01        0.00000    -1.63300203e+00       3.4199
     4    -8.54022966e-02        5.59126    -1.02062627e-01       1.1951
     8    -6.13735917e-03       13.91515    -6.37891419e-03       1.0394
    16    -3.94993112e-04       15.53789    -3.98682137e-04       1.0093
    32    -2.48603363e-05       15.88849    -2.49176335e-05       1.0023
    64    -1.55645818e-06       15.97238    -1.55735210e-06       1.0006
   128    -9.73205481e-08       15.99311    -9.73345060e-08       1.0001
   256    -6.08319262e-09       15.99827    -6.08340663e-09       1.0000
   512    -3.80214971e-10       15.99935    -3.80212914e-10       1.0000
  1024    -2.37658782e-11       15.99836    -2.37633071e-11       0.9999

The convergence rate is $O(h^4)$ as seen in third column; last column shows $\tilde E_n(f)/E_n(f)$ and the error estimate $\tilde E_n(f)$ becomes very good as $n$ increases.

9.4.3Compare Trapezoid and Simpson¶

The next function implements both Trapezoid and Simpson methods.

# Performs Trapezoid and Simpson quadrature
def integrate(a,b,n,f):
    h = (b-a)/n
    x = linspace(a,b,n+1)
    y = f(x)
    res1 = 0.5*y[0] + sum(y[1:n]) + 0.5*y[n] # Trapezoid
    res2 = 4.0*sum(y[1:n:2]) + 2.0*sum(y[2:n-1:2]) + y[0] + y[n] # Simpson
    return h*res1, (h/3.0)*res2

The next function performs convergence test.

def test(a,b,f,Ie,n,N):
    e1,e2 = zeros(N), zeros(N)
    for i in range(N):
        I1,I2 = integrate(a,b,n,f)
        e1[i],e2[i] = Ie - I1, Ie - I2
        if i > 0:
            print('%6d %18.8e %14.5g %18.8e %14.5g'%
                 (n,e1[i],e1[i-1]/e1[i],e2[i],e2[i-1]/e2[i]))
        else:
            print('%6d %18.8e %14.5g %18.8e %14.5g'%(n,e1[i],0,e2[i],0))
        n = 2*n

We will apply this to following examples.

Example 2

I = \int_0^1 x^3 \sqrt{x} \ud x = \frac{2}{9}

(18)

f = lambda x: x**3 * np.sqrt(x)
a, b = 0.0, 1.0
Ie = 2.0/9.0 # Exact integral
n, N = 2, 10
test(a,b,f,Ie,n,N)

     2    -7.19719516e-02              0    -3.37000954e-03              0
     4    -1.81666065e-02         3.9618    -2.31491460e-04         14.558
     8    -4.55322411e-03         3.9898    -1.54299774e-05         15.003
    16    -1.13906170e-03         3.9973    -1.00755946e-06         15.314
    32    -2.84814093e-04         3.9993    -6.48919993e-08         15.527
    64    -7.12066288e-05         3.9998    -4.14075488e-09         15.672
   128    -1.78018541e-05              4    -2.62556588e-10         15.771
   256    -4.45047596e-06              4    -1.65759628e-11          15.84
   512    -1.11261977e-06              4    -1.04333209e-12         15.888
  1024    -2.78154993e-07              4    -6.55309140e-14         15.921

Note that $f^{(4)}(x) = \order{x^{-\half}}$ and $\norm{f}_\infty = \infty$ but still we observe optimal convergence rates for both methods. This can be explained by deriving different error estimates using integral form of Taylor series, which we do in a later chapter.

Example 3

I = \int_0^5 \frac{\ud x}{1 + (x-\pi)^2} = \tan^{-1}(5 - \pi) + \tan^{-1}(\pi)

(19)

f = lambda x: 1.0/(1.0 + (x-np.pi)**2)
a, b = 0.0, 5.0
Ie = np.arctan(b-np.pi) + np.arctan(np.pi)
n, N = 2, 10
test(a,b,f,Ie,n,N)

     2     1.73111440e-01              0    -2.85329178e-01              0
     4     7.10986397e-02         2.4348     3.70943729e-02         -7.692
     8     7.49581780e-03         9.4851    -1.37051228e-02        -2.7066
    16     1.95340266e-03         3.8373     1.05930941e-04        -129.38
    32     4.89160655e-04         3.9934     1.07998844e-06         98.085
    64     1.22340738e-04         3.9983     6.74323797e-08         16.016
   128     3.05883472e-05         3.9996     4.21691837e-09         15.991
   256     7.64728450e-06         3.9999     2.63594480e-10         15.998
   512     1.91183348e-06              4     1.64752656e-11         15.999
  1024     4.77959142e-07              4     1.02984288e-12         15.998

The integrand is infinitely differentiable, but we do not observe proper convergence rate for small $n$ because the integrand has a peaky distribution. When $n$ is sufficiently large, we do observed the theoretically expected convergence rates.

Example 4

I = \int_0^1 \sqrt{x} \ud x = \frac{2}{3}

(20)

f = lambda x: np.sqrt(x)
a, b = 0.0, 1.0
Ie = 2.0/3.0
n, N = 2, 10
test(a,b,f,Ie,n,N)

     2     6.31132761e-02              0     2.85954792e-02              0
     4     2.33836204e-02          2.699     1.01404019e-02           2.82
     8     8.53644504e-03         2.7393     3.58738658e-03         2.8267
    16     3.08546979e-03         2.7667     1.26847804e-03         2.8281
    32     1.10773039e-03         2.7854     4.48483920e-04         2.8284
    64     3.95855288e-04         2.7983     1.58563588e-04         2.8284
   128     1.41009370e-04         2.8073     5.60607304e-05         2.8284
   256     5.01176901e-05         2.8136     1.98204636e-05         2.8284
   512     1.77851167e-05          2.818     7.00759224e-06         2.8284
  1024     6.30444768e-06          2.821     2.47755801e-06         2.8284

Since $f'(0)$ is not finite, we do not get the optimal convergence rates. But the errors still decrease and both methods converge at same rate of $\order{h^{1.5}}$ . See Lyness and Ninham (1967) and the discussion in Atkinson, 2004, Sec. 5.4, page 290-291.

Example 5

I = \int_0^{2\pi} \ee^{\cos x} \ud x = 7.95492652101284

(21)

f = lambda x: np.exp(np.cos(x))
a, b = 0.0, 2*np.pi
Ie = 7.95492652101284
n, N = 2, 5
test(a,b,f,Ie,n,N)

     2    -1.74053505e+00              0     7.20800573e-01              0
     4    -3.43969188e-02         50.601     5.34315792e-01          1.349
     8    -1.25168894e-06          27480     1.14639707e-02         46.608
    16    -3.55271368e-15     3.5232e+08     4.17229640e-07          27476
    32    -3.55271368e-15              1    -1.77635684e-15    -2.3488e+08

The integrand is periodic and the error formula suggests that we should expect fast convergence. Trapezoid is more accurate than Simpson, compare the errors between them for $n=8,16$ . Convergence rates are large, indicating exponential convergence. We will see later that for periodic functions, trapezoid method is the most accurate.

References¶

Atkinson, K. E. (2004). An Introduction to Numerical Analysis (2nd ed.). Wiley.

9.4 Simpson rule

9.4.1Single interval¶

9.4.2Composite Simpson rule¶

9.4.3Compare Trapezoid and Simpson¶