#%config InlineBackend.figure_format = 'svg'
from pylab import *
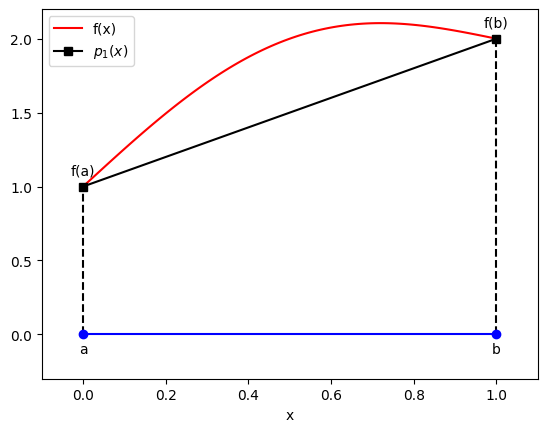
9.3.1 Single interval ¶ Consider a function f : [ a , b ] → R f : [a,b] \to \re f : [ a , b ] → R p 1 ( x ) p_1(x) p 1 ( x )
p 1 ( a ) = f ( a ) , p 1 ( b ) = f ( b ) p_1(a) = f(a), \qquad p_1(b) = f(b) p 1 ( a ) = f ( a ) , p 1 ( b ) = f ( b ) Then the approximate integral is
I 1 ( f ) = ∫ a b p 1 ( x ) d x = b − a 2 [ f ( a ) + f ( b ) ] I_1(f) = \int_a^b p_1(x) \ud x = \frac{b-a}{2}[f(a) + f(b)] I 1 ( f ) = ∫ a b p 1 ( x ) d x = 2 b − a [ f ( a ) + f ( b )] a, b = 0.0, 1.0
f = lambda x: 1.0 + x + 0.5* sin(pi*x)
x = linspace(a,b,100)
plot([a,a],[0,f(a)],'k--')
plot([b,b],[0,f(b)],'k--')
plot([a,b],[0,0],'bo-')
plot(x, f(x), 'r-', label='f(x)')
plot([a,b],[f(a),f(b)],'sk-',label='$p_1(x)$')
d = 0.05
text(a,-d,"a",ha='center',va='top')
text(b,-d,"b",ha='center',va='top')
text(a,f(a)+0.06,"f(a)",ha='center',va='bottom')
text(b,f(b)+0.06,"f(b)",ha='center',va='bottom')
axis([-0.1, 1.1, -0.3, 2.2])
legend(), xlabel('x');Note that this is the area under the straight line curve p 1 ( x ) p_1(x) p 1 ( x ) (30)
f ( x ) − p 1 ( x ) = ( x − a ) ( x − b ) f [ a , b , x ] f(x) - p_1(x) = (x-a)(x-b) f[a,b,x] f ( x ) − p 1 ( x ) = ( x − a ) ( x − b ) f [ a , b , x ] Then, the error in the integral is
E 1 ( f ) = ∫ a b [ f ( x ) − p 1 ( x ) ] d x = ∫ a b ( x − a ) ( x − b ) f [ a , b , x ] d x \begin{aligned}
E_1(f)
&= \int_a^b [f(x) - p_1(x)] \ud x \\
&= \int_a^b (x-a) (x-b) f[a,b,x] \ud x
\end{aligned} E 1 ( f ) = ∫ a b [ f ( x ) − p 1 ( x )] d x = ∫ a b ( x − a ) ( x − b ) f [ a , b , x ] d x If g g g [ a , b ] [a,b] [ a , b ] f f f
∫ a b f ( x ) g ( x ) d x = f ( c ) ∫ a b g ( x ) d x \int_a^b f(x) g(x)\ud x = f(c) \int_a^b g(x) \ud x ∫ a b f ( x ) g ( x ) d x = f ( c ) ∫ a b g ( x ) d x for some c ∈ [ a , b ] c \in [a,b] c ∈ [ a , b ]
Using integral mean value theorem
E 1 ( f ) = f [ a , b , ξ ] ∫ a b ( x − a ) ( x − b ) d x , for some ξ ∈ [ a , b ] E_1(f) = f[a,b,\xi] \int_a^b (x-a)(x-b) \ud x, \qquad \textrm{for some $\xi \in [a,b]$} E 1 ( f ) = f [ a , b , ξ ] ∫ a b ( x − a ) ( x − b ) d x , for some ξ ∈ [ a , b ] Finally, using the properties of divided differences (65)
E 1 ( f ) = [ 1 2 f ′ ′ ( η ) ] [ − 1 6 ( b − a ) 3 ] , for some η ∈ [ a , b ] = − 1 12 ( b − a ) 3 f ′ ′ ( η ) \begin{aligned}
E_1(f)
&= \left[ \half f''(\eta) \right] \left[ -\frac{1}{6} (b-a)^3 \right], \qquad \textrm{for some $\eta \in [a,b]$} \\
&= -\frac{1}{12} (b-a)^3 f''(\eta)
\end{aligned} E 1 ( f ) = [ 2 1 f ′′ ( η ) ] [ − 6 1 ( b − a ) 3 ] , for some η ∈ [ a , b ] = − 12 1 ( b − a ) 3 f ′′ ( η ) The error will be small only if b − a b-a b − a
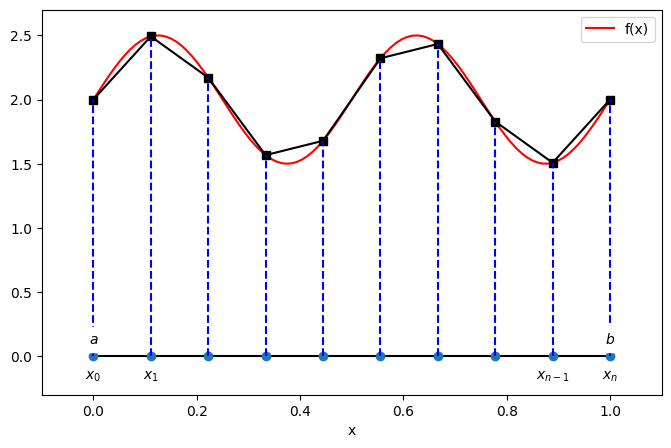
9.3.2 Composite trapezoidal rule ¶ Divide [ a , b ] [a,b] [ a , b ] n n n
a = x 0 < x 1 < … < x n = b with spacing h = b − a n a = x_0 < x_1 < \ldots < x_n = b \qquad \textrm{with spacing} \qquad h = \frac{b-a}{n} a = x 0 < x 1 < … < x n = b with spacing h = n b − a and
x j = a + j h , j = 0 , 1 , 2 , … , n x_j = a + j h, \qquad j=0,1,2,\ldots, n x j = a + jh , j = 0 , 1 , 2 , … , n figure(figsize=(8,5))
xp = linspace(0.0,1.0,10)
x = linspace(0,1,100)
f = lambda x: 2 + sin(2*pi*x)*cos(2*pi*x)
plot([0,1],[0,0],'k+-')
plot(xp,0*xp,'o')
plot(x,f(x),'r-',label='f(x)')
plot(xp,f(xp),'sk-')
for xx in xp:
plot([xx,xx],[0,f(xx)],'b--')
axis([-0.1,1.1,-0.3,2.7])
d = 0.1
text(xp[0],-d,'$x_0$',va='top',ha='center')
text(xp[1],-d,'$x_1$',va='top',ha='center')
text(xp[-2],-d,'$x_{n-1}$',va='top',ha='center')
text(xp[-1],-d,'$x_n$',va='top',ha='center')
text(0,d,'$a$',ha='center',backgroundcolor='white')
text(1,d,'$b$',ha='center',backgroundcolor='white')
legend(), xlabel('x');Let us use the Trapezoidal rule in each interval [ x j − 1 , x j ] [x_{j-1},x_j] [ x j − 1 , x j ]
I ( f ) = ∫ a b f ( x ) d x = ∑ j = 1 n ∫ x j − 1 x j f ( x ) d x I(f) = \int_a^b f(x) \ud x = \sum_{j=1}^n \int_{x_{j-1}}^{x_j} f(x) \ud x I ( f ) = ∫ a b f ( x ) d x = j = 1 ∑ n ∫ x j − 1 x j f ( x ) d x From the previous section, we know that
∫ x j − 1 x j f ( x ) d x = h 2 [ f ( x j − 1 ) + f ( x j ) ] − h 3 12 f ′ ′ ( η j ) , η j ∈ [ x j − 1 , x j ] \int_{x_{j-1}}^{x_j} f(x) \ud x = \frac{h}{2}[f(x_{j-1}) + f(x_j)] - \frac{h^3}{12}f''(\eta_j), \qquad \eta_j \in [x_{j-1}, x_j] ∫ x j − 1 x j f ( x ) d x = 2 h [ f ( x j − 1 ) + f ( x j )] − 12 h 3 f ′′ ( η j ) , η j ∈ [ x j − 1 , x j ] Hence
I ( f ) = ∑ j = 1 n h 2 [ f ( x j − 1 ) + f ( x j ) ] − ∑ j = 1 n h 3 12 f ′ ′ ( η j ) = I n ( f ) − ∑ j = 1 n h 3 12 f ′ ′ ( η j ) \begin{aligned}
I(f)
&= \clr{red}{ \sum_{j=1}^n \frac{h}{2}[f(x_{j-1}) + f(x_j)] }
- \sum_{j=1}^n \frac{h^3}{12}f''(\eta_j) \\
&= \clr{red}{ I_n(f) } - \sum_{j=1}^n \frac{h^3}{12}f''(\eta_j)
\end{aligned} I ( f ) = j = 1 ∑ n 2 h [ f ( x j − 1 ) + f ( x j )] − j = 1 ∑ n 12 h 3 f ′′ ( η j ) = I n ( f ) − j = 1 ∑ n 12 h 3 f ′′ ( η j ) where
I n ( f ) = h [ 1 2 f 0 + f 1 + f 2 + … + f n − 1 + 1 2 f n ] I_n(f) = h [ \shalf f_0 + f_1 + f_2 + \ldots + f_{n-1} + \shalf f_n] I n ( f ) = h [ 2 1 f 0 + f 1 + f 2 + … + f n − 1 + 2 1 f n ] is the composite Trapezoidal rule. The error is
E n ( f ) = I ( f ) − I n ( f ) = − h 3 12 ∑ j = 1 n f ′ ′ ( η j ) = − n h 3 12 1 n ∑ j = 1 n f ′ ′ ( η j ) ⏟ M n E_n(f) = I(f) - I_n(f) = - \frac{h^3}{12} \sum_{j=1}^n f''(\eta_j) = - \frac{n h^3}{12} \underbrace{\frac{1}{n} \sum_{j=1}^n f''(\eta_j)}_{M_n} E n ( f ) = I ( f ) − I n ( f ) = − 12 h 3 j = 1 ∑ n f ′′ ( η j ) = − 12 n h 3 M n n 1 j = 1 ∑ n f ′′ ( η j ) where
min x ∈ [ a , b ] f ′ ′ ( x ) ≤ min 1 ≤ j ≤ n f ′ ′ ( η j ) ≤ M n ≤ max 1 ≤ j ≤ n f ′ ′ ( η j ) ≤ max x ∈ [ a , b ] f ′ ′ ( x ) \min_{x \in [a,b]} f''(x) \le \min_{1 \le j \le n} f''(\eta_j) \le M_n \le \max_{1 \le j \le n} f''(\eta_j) \le \max_{x \in [a,b]} f''(x) x ∈ [ a , b ] min f ′′ ( x ) ≤ 1 ≤ j ≤ n min f ′′ ( η j ) ≤ M n ≤ 1 ≤ j ≤ n max f ′′ ( η j ) ≤ x ∈ [ a , b ] max f ′′ ( x ) If f ′ ′ ( x ) f''(x) f ′′ ( x )
⟹ ∃ η ∈ [ a , b ] such that M n = f ′ ′ ( η ) \implies \exists \eta \in [a,b] \qquad \textrm{such that} \qquad M_n = f''(\eta) ⟹ ∃ η ∈ [ a , b ] such that M n = f ′′ ( η ) Hence, after using n h = b − a nh=b-a nh = b − a
E n ( f ) = − 1 12 ( b − a ) h 2 f ′ ′ ( η ) , for some η ∈ [ a , b ] E_n(f) = - \frac{1}{12}(b-a) h^2 f''(\eta), \qquad \textrm{for some $\eta \in [a,b]$} E n ( f ) = − 12 1 ( b − a ) h 2 f ′′ ( η ) , for some η ∈ [ a , b ] The error goes to zero as n → ∞ n \to \infty n → ∞ h → 0 h \to 0 h → 0
If f ( x ) f(x) f ( x ) f ′ ′ = 0 f''=0 f ′′ = 0
The error of Trapezoidal rule converges quadratically
∣ E n ( f ) ∣ = O ( h 2 ) = O ( 1 n 2 ) |E_n(f)| = \order{h^2} = \order{\frac{1}{n^2}} ∣ E n ( f ) ∣ = O ( h 2 ) = O ( n 2 1 ) If n n n 1 4 \frac{1}{4} 4 1
E n ( f ) E 2 n ( f ) ≈ 1 / n 2 1 / ( 2 n ) 2 = 2 2 = 4 \frac{E_n(f)}{E_{2n}(f)} \approx \frac{1/n^2}{1/(2n)^2} = 2^2 = 4 E 2 n ( f ) E n ( f ) ≈ 1/ ( 2 n ) 2 1/ n 2 = 2 2 = 4 The next functions compute integral with composite trapezoidal rule.
# n intervals, n+1 points
def trapz1(a,b,n,f):
h = (b-a)/n
x = linspace(a,b,n+1)
y = f(x)
res = h * (sum(y[1:n]) + 0.5*(y[0] + y[n]))
return res
f ( x ) = x , x ∈ [ 0 , 1 ] ∫ 0 1 f ( x ) d x = 1 2 \begin{align}
f(x) &= x, \qquad x \in [0,1] \\
\int_0^1 f(x) \ud x &= \half
\end{align} f ( x ) ∫ 0 1 f ( x ) d x = x , x ∈ [ 0 , 1 ] = 2 1 f = lambda x: x
print("Integral = ", trapz1(0.0,1.0,10,f))f ( x ) = x 2 , x ∈ [ 0 , 1 ] ∫ 0 1 f ( x ) d x = 1 3 \begin{align}
f(x) &= x^2, \qquad x \in [0,1] \\
\int_0^1 f(x) \ud x &= \frac{1}{3}
\end{align} f ( x ) ∫ 0 1 f ( x ) d x = x 2 , x ∈ [ 0 , 1 ] = 3 1 f = lambda x: x**2
print("Integral = ", trapz1(0.0,1.0,10,f))Integral = 0.3350000000000001
f ( x ) = exp ( x ) cos ( x ) , x ∈ [ 0 , π ] ∫ 0 1 f ( x ) d x = − 1 2 ( 1 + exp ( π ) ) \begin{align}
f(x) &= \exp(x)\cos(x), \qquad x \in [0,\pi] \\
\int_0^1 f(x) \ud x &= -\frac{1}{2}(1+\exp(\pi))
\end{align} f ( x ) ∫ 0 1 f ( x ) d x = exp ( x ) cos ( x ) , x ∈ [ 0 , π ] = − 2 1 ( 1 + exp ( π )) f = lambda x: exp(x)*cos(x)
qe = -0.5*(1.0 + exp(pi)) # Exact integral
n,N = 4,10
e = zeros(N)
for i in range(N):
e[i] = trapz1(0.0,pi,n,f) - qe
if i > 0:
print('%6d %24.14e %14.5e'%(n,e[i],e[i-1]/e[i]))
else:
print('%6d %24.14e'%(n,e[i]))
n = 2*n 4 -1.26567653098185e+00
8 -3.11816113365945e-01 4.05905e+00
16 -7.76577835071954e-02 4.01526e+00
32 -1.93958006245669e-02 4.00385e+00
64 -4.84778281250620e-03 4.00096e+00
128 -1.21187271271594e-03 4.00024e+00
256 -3.02963615787633e-04 4.00006e+00
512 -7.57406187865683e-05 4.00002e+00
1024 -1.89351368735657e-05 4.00000e+00
2048 -4.73378310594796e-06 4.00000e+00
The last column shows E n ( f ) / E 2 n ( f ) E_n(f)/E_{2n}(f) E n ( f ) / E 2 n ( f ) O ( h 2 ) \order{h^2} O ( h 2 )
9.3.3 Asymptotic error estimate ¶ We can estimate the error as
∣ E n ( f ) ∣ ≤ 1 12 ( b − a ) h 2 max x ∈ [ a , b ] ∣ f ′ ′ ( x ) ∣ |E_n(f)| \le \frac{1}{12}(b-a) h^2 \max_{x \in [a,b]}|f''(x)| ∣ E n ( f ) ∣ ≤ 12 1 ( b − a ) h 2 x ∈ [ a , b ] max ∣ f ′′ ( x ) ∣ provided we can estimate the second derivative. A more useful error estimate can be derived as follows.
Using the error of the composite rule, we can compute the limit
lim n → ∞ E n ( f ) h 2 = − 1 12 lim n → ∞ h ∑ j = 1 n f ′ ′ ( η j ) , η j ∈ [ x j − 1 , x j ] = − 1 12 ∫ a b f ′ ′ ( x ) d x = − 1 12 [ f ′ ( b ) − f ′ ( a ) ] \begin{aligned}
\lim_{n \to \infty} \frac{E_n(f)}{h^2}
&= - \frac{1}{12} \lim_{n \to \infty} h \sum_{j=1}^n f''(\eta_j), \qquad \eta_j \in [x_{j-1}, x_j] \\
&= -\frac{1}{12} \int_a^b f''(x) \ud x \\
&= -\frac{1}{12}[f'(b) - f'(a)]
\end{aligned} n → ∞ lim h 2 E n ( f ) = − 12 1 n → ∞ lim h j = 1 ∑ n f ′′ ( η j ) , η j ∈ [ x j − 1 , x j ] = − 12 1 ∫ a b f ′′ ( x ) d x = − 12 1 [ f ′ ( b ) − f ′ ( a )] Hence for large n n n
E n ( f ) ≈ − h 2 12 [ f ′ ( b ) − f ′ ( a ) ] = : E ~ n ( f ) E_n(f) \approx -\frac{h^2}{12}[f'(b) - f'(a)] =: \tilde E_n(f) E n ( f ) ≈ − 12 h 2 [ f ′ ( b ) − f ′ ( a )] =: E ~ n ( f ) 9.3.4 Corrected trapezoidal rule ¶ Using the asymptotic error estimate
I ( f ) − I n ( f ) ≈ E ~ n ( f ) = − h 2 12 [ f ′ ( b ) − f ′ ( a ) ] ⟹ I ( f ) ≈ I n ( f ) − h 2 12 [ f ′ ( b ) − f ′ ( a ) ] \begin{gather}
I(f) - I_n(f) \approx \tilde E_n(f) = -\frac{h^2}{12}[f'(b) - f'(a)] \\
\implies I(f) \approx I_n(f) -\frac{h^2}{12}[f'(b) - f'(a)]
\end{gather} I ( f ) − I n ( f ) ≈ E ~ n ( f ) = − 12 h 2 [ f ′ ( b ) − f ′ ( a )] ⟹ I ( f ) ≈ I n ( f ) − 12 h 2 [ f ′ ( b ) − f ′ ( a )] we can define a corrected Trapezoidal rule as
C n ( f ) = I n ( f ) − h 2 12 [ f ′ ( b ) − f ′ ( a ) ] = h [ 1 2 f 0 + f 1 + f 2 + … + f n − 1 + 1 2 f n ] − h 2 12 [ f ′ ( b ) − f ′ ( a ) ] \begin{align}
C_n(f) &= I_n(f) -\frac{h^2}{12}[f'(b) - f'(a)] \\
&= h \left[ \shalf f_0 + f_1 + f_2 + \ldots + f_{n-1} + \shalf f_n \right] - \frac{h^2}{12}[f'(b) - f'(a)]
\end{align} C n ( f ) = I n ( f ) − 12 h 2 [ f ′ ( b ) − f ′ ( a )] = h [ 2 1 f 0 + f 1 + f 2 + … + f n − 1 + 2 1 f n ] − 12 h 2 [ f ′ ( b ) − f ′ ( a )] Consider the integral
I = ∫ 0 π e x cos x d x I = \int_0^\pi \ee^x \cos x \ud x I = ∫ 0 π e x cos x d x The exact value is
I = − 1 2 ( 1 + e π ) ≈ − 12.0703463164 I = -\half (1 + \ee^\pi) \approx -12.0703463164 I = − 2 1 ( 1 + e π ) ≈ − 12.0703463164 The next function implements both trapezoid and the corrected rule.
# n = number of intervals
# There are n+1 points
def trapz2(a,b,n,f,df):
h = (b-a)/n
x = linspace(a,b,n+1)
y = f(x)
res = sum(y[1:n]) + 0.5*(y[0] + y[n])
return h*res, h*res - (h**2/12)*(df(b) - df(a))
f = lambda x: exp(x)*cos(x)
df = lambda x: exp(x)*(cos(x) - sin(x))
qe = -0.5*(1.0 + exp(pi)) # Exact integral
n,N = 4,10
e1,e2 = zeros(N),zeros(N)
for i in range(N):
e1[i],e2[i] = trapz2(0.0,pi,n,f,df) - qe
if i > 0:
print('%6d %24.14e %10.5f %24.14e %10.5f' %
(n,e1[i],e1[i-1]/e1[i],e2[i],e2[i-1]/e2[i]))
else:
print('%6d %24.14e %10.5f %24.14e %10.5f' %
(n,e1[i],0,e2[i],0))
n = 2*n 4 -1.26567653098185e+00 0.00000 -2.47437900765224e-02 0.00000
8 -3.11816113365945e-01 4.05905 -1.58292813961225e-03 15.63166
16 -7.76577835071954e-02 4.01526 -9.94872006128134e-05 15.91087
32 -1.93958006245669e-02 4.00385 -6.22654792081789e-06 15.97791
64 -4.84778281250620e-03 4.00096 -3.89293344227326e-07 15.99449
128 -1.21187271271594e-03 4.00024 -2.43329250082525e-08 15.99863
256 -3.02963615787633e-04 4.00006 -1.52084034255040e-09 15.99966
512 -7.57406187865683e-05 4.00002 -9.50493017626286e-11 16.00054
1024 -1.89351368735657e-05 4.00000 -5.94013727095444e-12 16.00120
2048 -4.73378310594796e-06 4.00000 -3.73034936274053e-13 15.92381
As seen in last column, the error in the corrected rule converges at a rate of 16, i.e., as O ( h 4 ) \order{h^4} O ( h 4 )