Numerical Integration - Numerical Analysis

from pylab import *

8.1Problem of quadrature¶

The problem is to compute the numerical value of the definite integral

I(f) = \int_a^b f(x) \ud x

(1)

where $f:[a,b] \to \re$ is a given function. The solution to this problem usually takes the following form: Form a partition or grid

a \le x_0 \le x_1 \le \ldots \le x_n \le b

(2)

figure(figsize=(8,5))
xp = linspace(0.05,0.95,10)
x  = linspace(0,1,100)
f  = lambda x: 2 + sin(2*pi*x)*cos(2*pi*x)
plot([0,1],[0,0],'k+-')
plot(xp,0*xp,'o')
plot(x,f(x),'r-',label='f(x)')
plot(xp,f(xp),'sk')
for xx in xp:
    plot([xx,xx],[0,f(xx)],'b--')
axis([-0.1,1.1,-0.3,2.7])
d = 0.1
text(xp[0],-d,'$x_0$',va='top',ha='center')
text(xp[1],-d,'$x_1$',va='top',ha='center')
text(xp[-2],-d,'$x_{n-1}$',va='top',ha='center')
text(xp[-1],-d,'$x_n$',va='top',ha='center')
text(0,d,'$x=a$',ha='center')
text(1,d,'$x=b$',ha='center')
legend(), xlabel('x');

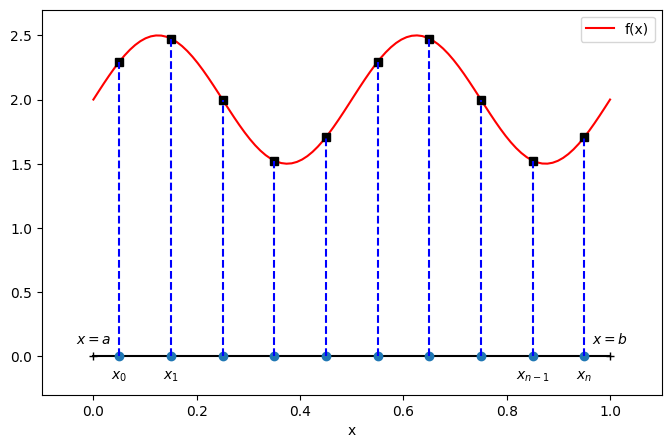
and approximate the integral by a formula of the type

I_n(f) = \sum_{j=0}^n w_j f(x_j)

(3)

where the $\{ w_j \}$ are some weights. We may be interested in the following type of questions.

Given the nodes $\{ x_j \}$ how to find the weights to obtain a good approximation ?
Can we find both the nodes and weights so that the formula is as accurate as possible ?

To measure the accuracy, we may establish a result like

|I(f) - I_n(f)| = \order{\frac{1}{n^p}}, \qquad \textrm{for some $p > 0$}

(4)

Then the approximations converge fast if $p$ is very large and this is algebraic convergence. A still better approximation is one which would converge exponentially

|I(f) - I_n(f)| = \order{\ee^{-\alpha n}}, \qquad \textrm{for some $\alpha > 0$}

(5)

8.2Integration via function approximation¶

Let $\{ f_n \}$ be a family of approximations to $f$ such that

\lim_{n \to \infty} \norm{f - f_n}_\infty = 0

(6)

i.e., they converge uniformly an also in a pointwise sense. Define the quadrature rule

I_n(f) = \int_a^b f_n(x) \ud x = I(f_n)

(7)

Then the error in the integral is

E_n(f) = I(f) - I_n(f) = \int_a^b [f(x) - f_n(x)] \ud x

(8)

so that

|E_n(f)| \le \int_a^b |f(x) - f_n(x)| \ud x \le (b-a) \norm{f - f_n}_\infty

(9)

We thus automatically obtain convergence of the integral approximations.

8Numerical Integration

8.1Problem of quadrature¶

8.2Integration via function approximation¶