ODE with periodic solution - Numerical Analysis

from pylab import *

Consider the ODE system

\begin{gather} x' = -y, \qquad y' = x \\ x(0) = 1, \qquad y(0) = 0 \end{gather}

(1)

The exact solution is

x(t) = \cos(t), \qquad y(t) = \sin(t)

(2)

This solution is periodic. It also has a quadratic invariant

x^2(t) + y^2(t) = 1, \qquad \forall t

(3)

theta = linspace(0.0, 2*pi, 500)
xe = cos(theta)
ye = sin(theta)

10.11.1Forward Euler scheme¶

def ForwardEuler(h,T):
    N = int(T/h)
    x,y = zeros(N),zeros(N)
    x[0] = 1.0
    y[0] = 0.0
    for n in range(1,N):
        x[n] = x[n-1] - h*y[n-1]
        y[n] = y[n-1] + h*x[n-1]
    return x,y

h = 0.02
T = 4.0*pi
x,y = ForwardEuler(h,T)

plot(xe,ye,'r--',label='Exact')
plot(x,y,label='FE')
legend()
grid(True)
gca().set_aspect('equal')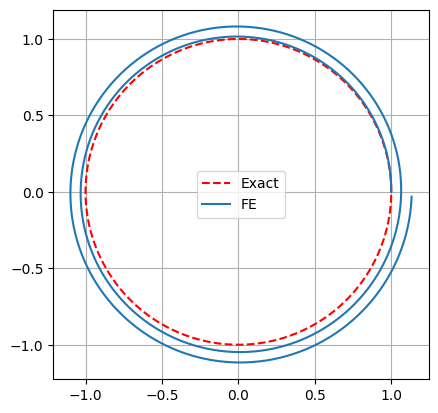

The phase space trajectory is spiralling outward.

10.11.2Backward Euler scheme¶

x_n = x_{n-1} - h y_n, \qquad y_n = y_{n-1} + h x_n

(4)

Eliminate $y_n$ from first equation and solve for $x_n$ to get

x_n = \frac{x_{n-1} - h y_{n-1}}{1 + h^2}

(5)

and now $y_n$ can also be computed.

def BackwardEuler(h,T):
    N = int(T/h)
    x,y = zeros(N),zeros(N)
    x[0] = 1.0
    y[0] = 0.0
    for n in range(1,N):
        x[n] = (x[n-1] - h*y[n-1])/(1.0 + h**2)
        y[n] = y[n-1] + h*x[n]
    return x,y

h = 0.02
T = 4.0*pi
x,y = BackwardEuler(h,T)

plot(xe,ye,'r--',label='Exact')
plot(x,y,label='BE')
legend()
grid(True)
gca().set_aspect('equal')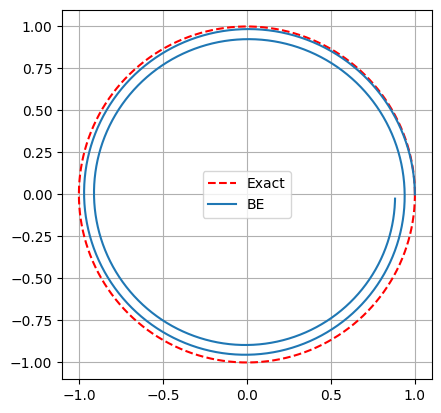

The phase space trajectory is spiralling inward.

10.11.3Trapezoidal scheme¶

x_n = x_{n-1} - \frac{h}{2}(y_{n-1} + y_n), \qquad y_n = y_{n-1} + \frac{h}{2}(x_{n-1} + x_n)

(6)

Eliminate $y_n$ from first equation

x_n = \frac{ (1-\frac{1}{4}h^2) x_{n-1} - h y_{n-1} }{1 + \frac{1}{4}h^2}

(7)

and now $y_n$ can also be computed.

def Trapezoid(h,T):
    N = int(T/h)
    x,y = zeros(N),zeros(N)
    x[0] = 1.0
    y[0] = 0.0
    for n in range(1,N):
        x[n] = ((1.0-0.25*h**2)*x[n-1] - h*y[n-1])/(1.0 + 0.25*h**2)
        y[n] = y[n-1] + 0.5*h*(x[n-1] + x[n])
    return x,y

h = 0.02
T = 4.0*pi
x,y = Trapezoid(h,T)

plot(xe,ye,'r--',label='Exact')
plot(x,y,label='Trap')
legend()
grid(True)
gca().set_aspect('equal')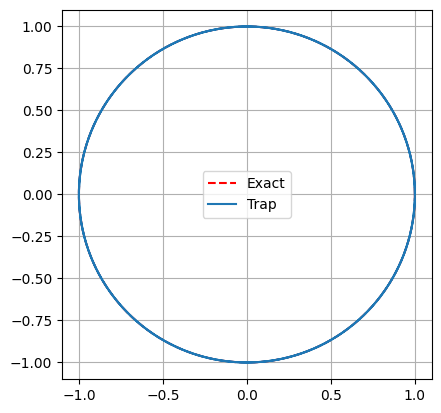

The phase space trajectory is exactly the unit circle.

Multiply first equation by $x_n + x_{n-1}$ and second equation by $y_n + y_{n-1}$

(x_n + x_{n-1})(x_n - x_{n-1}) = - \frac{h}{2}(x_n + x_{n-1})(y_n + y_{n-1})

(8)

(y_n + y_{n-1})(y_n - y_{n-1}) = + \frac{h}{2}(x_n + x_{n-1})(y_n + y_{n-1})

(9)

Adding the two equations we get

x_n^2 + y_n^2 = x_{n-1}^2 + y_{n-1}^2

(10)

Thus the Trapezoidal method is able to preserve the invariant.

10.11.4Partitioned Euler¶

This is a symplectic Runge-Kutta method. $x$ is updated explicitly and $y$ is updated implicitly.

x_n = x_{n-1} - h y_{n-1}, \qquad y_n = y_{n-1} + h x_{n}

(11)

The update of $y$ uses the latest updated value of $x$ .

def PartEuler(h,T):
    N = int(T/h)
    x,y = zeros(N),zeros(N)
    x[0] = 1.0
    y[0] = 0.0
    for n in range(1,N):
        x[n] = x[n-1] - h * y[n-1]
        y[n] = y[n-1] + h * x[n]
    return x,y

h = 0.02
T = 4.0*pi
x,y = PartEuler(h,T)

plot(xe,ye,'r--',label='Exact')
plot(x,y,label='PE')
legend()
grid(True)
gca().set_aspect('equal')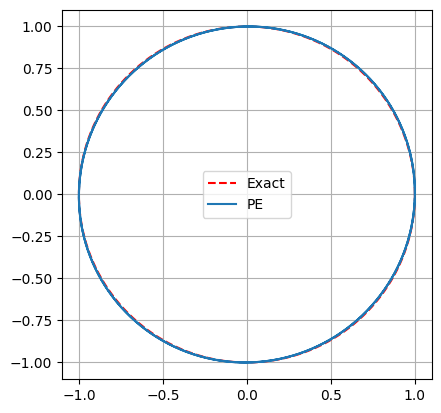

We get very good results, even though the method is only first order. We can also switch the implicit/explicit parts

y_n = y_{n-1} + h x_{n-1}, \qquad x_n = x_{n-1} - h y_n

(12)

10.11.5Classical RK4 scheme¶

def rhs(u):
    return array([u[1], -u[0]])

def RK4(h,T):
    N = int(T/h)
    u = zeros((N,2))
    u[0,0] = 1.0 # x
    u[0,1] = 0.0 # y
    for n in range(0,N-1):
        w = u[n,:]
        k0 = rhs(w)
        k1 = rhs(w + 0.5*h*k0)
        k2 = rhs(w + 0.5*h*k1)
        k3 = rhs(w + h*k2)
        u[n+1,:] = w + (h/6)*(k0 + k1 + k2 + k3)
    return u[:,0], u[:,1]

We test this method for a longer time.

h = 0.02
T = 10.0*pi
x,y = RK4(h,T)

plot(xe,ye,'r--',label='Exact')
plot(x,y,label='RK4')
legend()
grid(True)
gca().set_aspect('equal')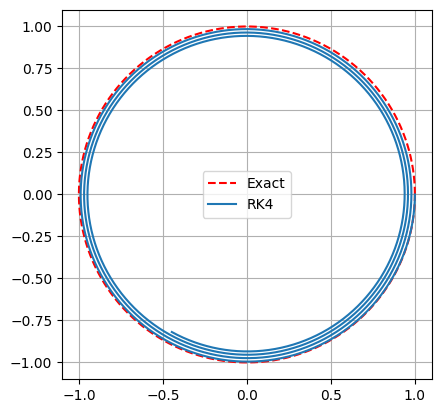

RK4 is a more accurate method compared to forward/backward Euler schemes, but it still loses total energy. The trajectory spirals inwards towards the origin.