Asymptotic stability: Adams, BDF

10.7.1Stability domains of Adams methods¶

See here for the schemes

For stability we require the roots $w$ of

\rho(w) - z \sigma(w)

(1)

to be less than one

|w_i(z)| < 1

(2)

We find the values of $z$ for which $|w|=1$

w = e^{i \theta}, \qquad z = \frac{\rho(e^{i\theta})}{\sigma(e^{i\theta})}

(3)

import numpy as np
from matplotlib import pyplot as plt

def AB2(theta):
    w = np.exp(1j*theta)
    return (w**2 - w)/(3.0*w/2.0 - 1.0/2.0)

def AB3(theta):
    w = np.exp(1j*theta)
    return (w**3 - w**2)/(23.0*w**2/12.0 - 4.0*w/3.0 + 5.0/12.0)

theta = np.linspace(0,2*np.pi,1000)

z = AB2(theta)
plt.plot(np.real(z),np.imag(z))

z = AB3(theta)
plt.plot(np.real(z),np.imag(z))

plt.legend(("AB2","AB3"))
plt.grid(True)
plt.xlim([-2, 1])
plt.ylim([-1, 1])
plt.axis('equal');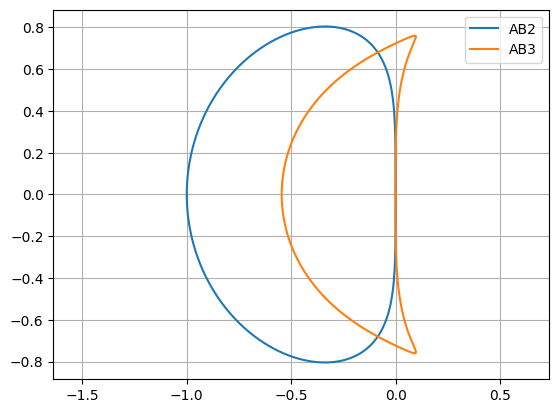

def AM3(theta):
    w = np.exp(1j*theta)
    return (w**2 - w)/(5.0*w**2/12.0 + 2.0*w/3.0 - 1.0/12.0)

def AM4(theta):
    w = np.exp(1j*theta)
    return (w**3 - w**2)/(3.0*w**3/8.0 + 19.0*w**2/24.0 - 5.0*w/24.0 + 1.0/24.0)

z = AM3(theta)
plt.plot(np.real(z),np.imag(z))

z = AM4(theta)
plt.plot(np.real(z),np.imag(z))

plt.legend(("AM3","AM4"))
plt.xlim([-7, 2])
plt.ylim([-4, 4])
plt.grid(True)
plt.axis('equal');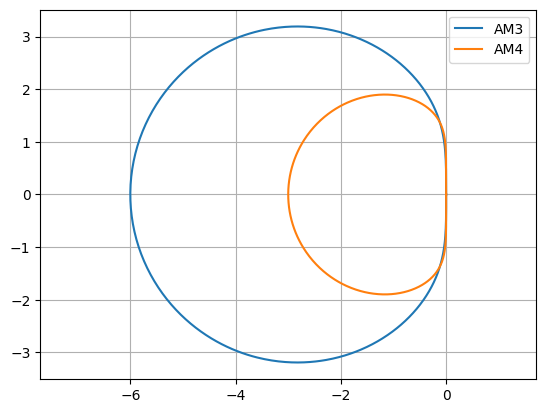

These discs are bigger than those for the AB methods, but they are also not A-stable methods. The imaginary axis is not contained in their stability domains, so these methods cannot be used for hyperbolic problems.

10.7.2Stability domains for BDF methods¶

See here for the schemes

Backward differentiation formula

def BDF1(theta):
    w = np.exp(1j*theta)
    return (w-1)/w

def BDF2(theta):
    w = np.exp(1j*theta)
    return (w**2 - 4.0*w/3.0 + 1.0/3.0)/(2.0*w**2/3.0)

def BDF3(theta):
    w = np.exp(1j*theta)
    return (w**3 - 18.0*w**2/11.0 + 9.0*w/11.0 - 2.0/11.0)/(6.0*w**3/11.0)

def BDF4(theta):
    w = np.exp(1j*theta)
    return (w**4 - 48.0*w**3/25.0 + 36.0*w**2/25.0 - 16.0*w/25.0 + 3.0/25.0)/(12.0*w**4/25.0)

z = BDF1(theta)
plt.plot(np.real(z),np.imag(z))

z = BDF2(theta)
plt.plot(np.real(z),np.imag(z))

z = BDF3(theta)
plt.plot(np.real(z),np.imag(z))

z = BDF4(theta)
plt.plot(np.real(z),np.imag(z))

plt.legend(("BDF1","BDF2","BDF3","BDF4"))
plt.xlim([-1, 18])
plt.ylim([-8, 8])
plt.grid(True)
plt.axis('equal');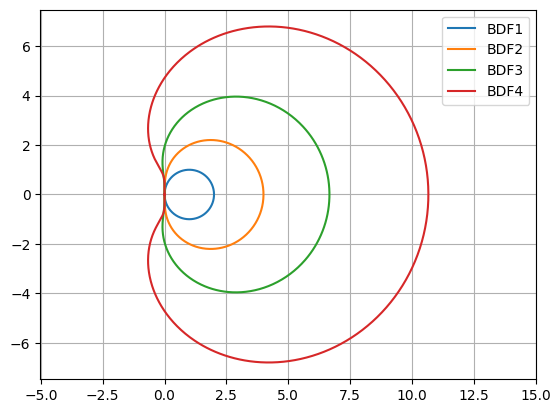

The region of asymptotic stability is the exterior of these discs. Only the BDF1 and BDF2 discs are entirely to the right of the imaginary axis and these are A-stable.

10.7 Asymptotic stability: Adams, BDF

10.7.1Stability domains of Adams methods¶

10.7.2Stability domains for BDF methods¶