Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

10.13 Nonlinear BVP using finite difference method

from pylab import *

Consider the BVP

y′′−2(y′)2y+y=0,x∈(−1,+1)y'' - 2 \frac{(y')^2}{y} + y = 0, \qquad x \in (-1,+1)
(1)

with boundary conditions

y(−1)=y(1)=1e+e−1y(-1) = y(1) = \frac{1}{e + e^{-1}}
(2)

The exact solution is given by

y(x)=1exp⁡(x)+exp⁡(−x)y(x) = \frac{1}{\exp(x) + \exp(-x)}
(3)

10.13.1Finite difference method

Make a uniform grid of n+1n+1 points such that

xj=−1+jh,0≤j≤n,h=2/nx_j = -1 + j h, \qquad 0 \le j \le n, \qquad h = 2/n
(4)

Then we approximate the differential equation by finite differences

ϕj=yj−1−2yj+yj+1h2−2yj(yj+1−yj−12h)2+yj=0,1≤j≤n−1\phi_j = \frac{y_{j-1}-2y_j + y_{j+1}}{h^2} - \frac{2}{y_j} \left(\frac{y_{j+1} - y_{j-1}}{2h}\right)^2 + y_j = 0, \quad 1 \le j \le n-1
(5)

with the boundary condition

y0=yn=1e+e−1y_0 = y_n = \frac{1}{e + e^{-1}}
(6)

This is a non-linear system of equations. We can eliminate y0,yny_0, y_n and form a problem to find the remaining unknowns. Define

Y=[y1,…,yn−1],ϕ=[ϕ1,…,ϕn−1]Y = [y_1, \ldots, y_{n-1}], \qquad \phi = [\phi_1, \ldots, \phi_{n-1}]
(7)

Then ϕ=ϕ(Y)\phi = \phi(Y) is a map from Rn−1R^{n-1} to Rn−1R^{n-1}. The Newton method is given by

ϕ′(Yk)δYk=−ϕ(Yk),Yk+1=Yk+δYk\phi'(Y^k) \delta Y^k = - \phi(Y^k), \qquad Y^{k+1} = Y^k + \delta Y^k
(8)

The Jacobian is given by

[ϕ′]jl=∂ϕj∂yl,1≤j,l≤n−1[\phi']_{jl} = \frac{\partial \phi_j}{\partial y_l}, \quad 1 \le j,l \le n-1
(9)

and it is a tri-diagonal matrix, since ϕj\phi_j depends only on yj−1,yj,yj+1y_{j-1}, y_j, y_{j+1}.

def yexact(x):
    return 1.0/(exp(x)+exp(-x))

# Computes the vector phi(y): length (n-1)
# y = [y0, y1, ..., yn] = length n+1
def phi(y):
    n   = len(y) - 1
    h   = 2.0/n
    res = zeros(n-1)
    for i in range(1,n):
        dy = (y[i+1] - y[i-1])/(2.0*h)
        res[i-1] = (y[i-1] - 2.0*y[i] + y[i+1])/h**2 - 2.0*dy**2/y[i] + y[i]
    return res

# Computes Jacobian d(phi)/dy: (n-1)x(n-1)
# y = [y0, y1, ..., yn] = length n+1
def dphi(y):
    n   = len(y) - 1
    h   = 2.0/n
    res = zeros((n-1,n-1))
    for i in range(1,n):
        dy = (y[i+1] - y[i-1])/(2.0*h)
        if i > 1:
            res[i-1,i-2] = 1.0/h**2 + 4.0*dy/y[i]
        res[i-1,i-1] = -2.0/h**2 + 1.0 - 2.0*(dy/y[i])**2
        if i < n-1:
            res[i-1,i] = 1.0/h**2 - 4.0*dy/y[i]
    return res

We now solve the problem with Newton method.

n = 50

# Initial guess for y
y = zeros(n+1)
y[:] = 1.0/(exp(1) + exp(-1))

maxiter = 100
TOL = 1.0e-6
it = 0
while it < maxiter:
    b = -phi(y)
    if linalg.norm(b) < TOL:
        break
    A = dphi(y)
    v = linalg.solve(A,b)
    y[1:n] = y[1:n] + v
    it += 1
print("Number of iterations = %d" % it)
x = linspace(-1.0,1.0,n+1)
plot(x,y,'o',x,yexact(x))
legend(("Numerical","Exact"))
xlabel("x"), ylabel("y");
Number of iterations = 13
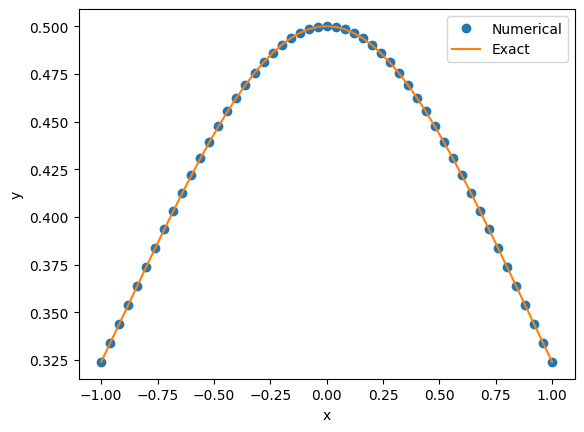
<Figure size 640x480 with 1 Axes>

Note that y is initially filled with boundary condition and then we update only the other values y[1:n] with Newton method. Thus during the Newton updates, y always satisfies the boundary condition.

Numerical Analysis
Shooting method for BVP